Why Positional Encoding?
Unlike recurrent neural networks (RNNs), transformers process tokens in parallel meaning they do not inherently understand the order of words in a sequence. In language, the meaning of a word can heavily depend on its position, for example, “Salt has important minerals.” and “The food is so bland I had to salt it.”. Salt is used as a noun and verb depending on it position on the sentence.
Positional encoding in a transformer are typically added to the word embeddings of each token, effectively injecting positional information into the model’s representation. For the input text “The cat ate the mouse.”, a transformer cannot understand the positional structure of the input sequence. Without positional encoding, the transformer will understand the input to be similar as “The mouse ate the cat.” or “The the ate mouse cat.”.
What’s RoPE?
No! It is not the one we use to tie things. RoPE also called Rotary Position Embedding is an elegant way to encode relative position information without explicitly storing positional difference.
It blends the concepts of absolute and relative positional encodings in a clever way.
- Absolute Positional Encoding: Each token is assigned a unique positional embedding. It can be a trainable vector or sinuisodal.
- Relative Positional Encoding: The key difference with RoPE is that it also encodes relative positions between tokens. However, it doesn’t explicitly store the positional differences like in traditional relative encoding methods. Instead, rotations are used to capture these relative distances between tokens.
Mathematical Foundation
To get a solid grasp of what RoPE does, we need to thake a little trip back in time to one of the most elegant mathematician, Euler, and his formula😅. If you have a foundation in complex numbers, you’ve probably seen this before:
$$ e^{i \theta} = \cos {\theta} + i \sin {\theta} $$This formula is the basis of understanding rotation in the complex plane. On the LHS, is a complex exponential describing a rotation by an angle $ \theta $ in the 2D plane. On the RHS, we have the real and imaginary component of the rotated point.
Now, remember a complex number is a combination of two real numbers $z = x +iy$ where $i$ is the imaginary unit and $x$, $y$ are the real numbers. These real numbers can be thought of as coordinates in the 2D plane and $z$ as a vector from the origin.
When we multiply a complex number by a complex exponential $e^{i \theta}$, we are rotating the point in the complex plane by an angle $\theta$.
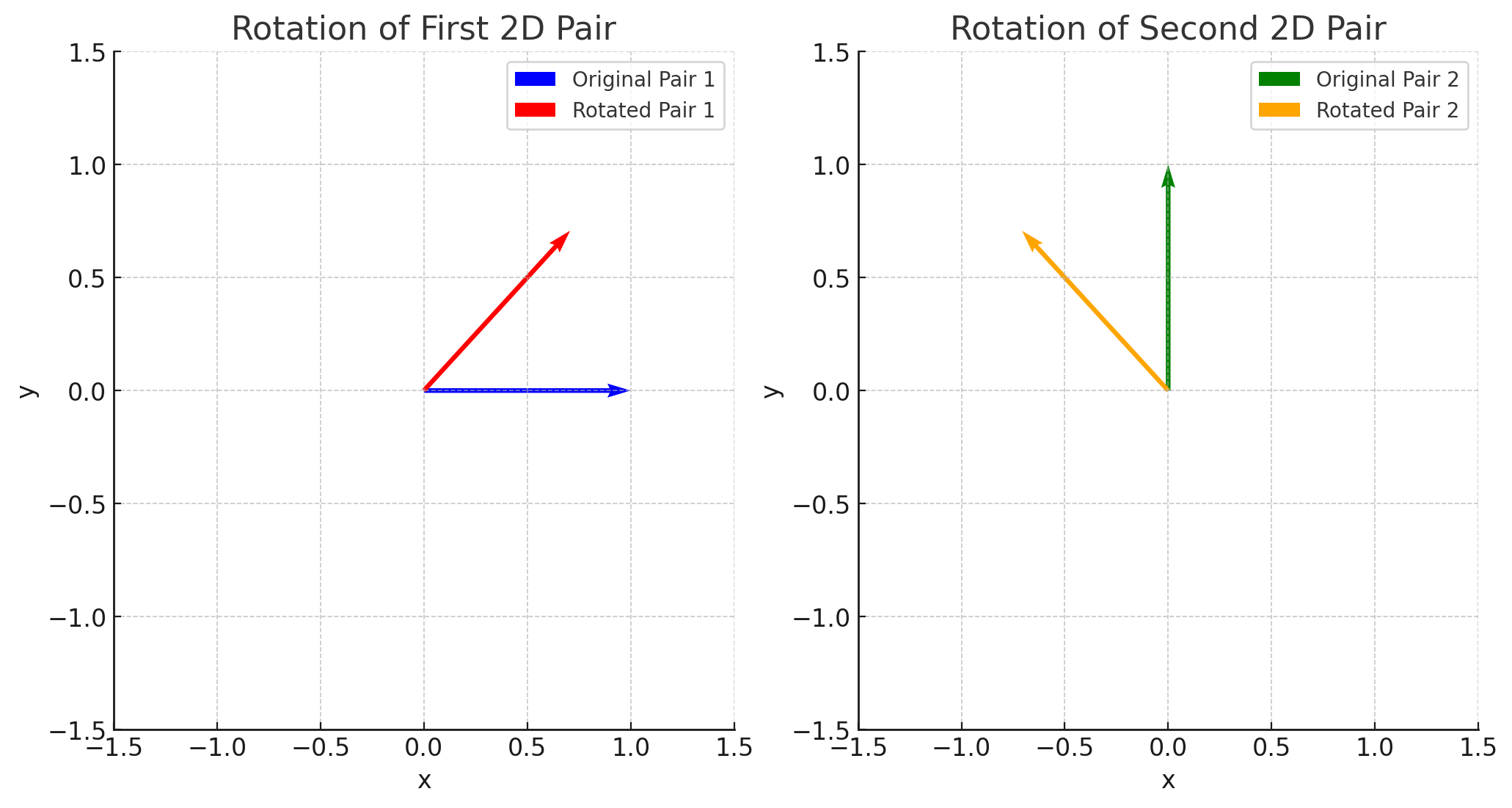
$$ \begin{aligned} &z^{'} = z \cdot e^{i \theta} & \\ &= (x +iy) \cdot (\cos {\theta} + i \sin {\theta}) & \\ &= x \cos {\theta} - y\sin {\theta} + i({x \sin {\theta} + y\cos {\theta}}) & \\ &=\begin{pmatrix} \cos {\theta} & -\sin {\theta}\\ \sin {\theta} & \cos {\theta} \end{pmatrix} \cdot \begin{bmatrix}x \\ y \end{bmatrix} \\ \end{aligned} $$This decomposition into magnitude (radial) and angle (angular) components will be critical for understanding the mechanics of RoPE.
Idea
In transformer’s architecture, information about individual tokens in conveyed through self-attention.
$$ Attention = softmax(\frac{Q.K^T}{\sqrt{d_k}}) \cdot V $$To incorporate relative position information into the attention mechanism, we find the inner product between the query token, $q_{m}$, at position $m$ and the key token, $k_{n}$, at position $n$,
$$ g(x_m, x_n, m - n) = \langle f_q(x_m, m), f_k(x_n, n) \rangle $$with $x_{m}$ being the embedding of the query token and $x_{n}$ being the embedding of the key token.
Rotation in the 2D case
For simplicity, let’s first look ar the 2D case. Using the insight from 1.1, the encoded query and key are defined as:
$$ \begin{align} f_q(x_m, m) &= (W_q x_m) e^{im\theta} \\ f_k(x_n, n) &= (W_k x_n) e^{in\theta} \end{align} $$The inner product between the query and key becomes:
$$ g(x_m, x_n, m - n) = \text{Re}[(W_q x_m)(W_k x_n)^* e^{i(m-n)\theta}] $$Here, the radial components $(W_{q}x_{m})$ and $(W_{k}x_{n})$ will remain independent of position $m$ or $n$. This independence is critical because it ensures that only the angular componenents $e^{im\theta}$ and $e^{in\theta}$ encode the positional differences.
The radial independence has been proven in the paper as:
$$ R_q(x_q, m) = R_q(x_q, 0) = \|q\|, \quad R_k(x_k, n) = R_k(x_k, 0) = \|k\|. $$Simplified, the magnitude of the query and key vectors remain the same even in different positions.
Therefore, rotation of the query and key can be expressed as:
$$ f_{q,k}(x_m, m) = \begin{pmatrix} \cos m\theta & -\sin m\theta \\ \sin m\theta & \cos m\theta \end{pmatrix} \begin{pmatrix} W_{q,k}^{(11)} & W_{q,k}^{(12)} \\ W_{q,k}^{(21)} & W_{q,k}^{(22)} \end{pmatrix} \begin{pmatrix} x_m^{(1)} \\ x_m^{(2)} \end{pmatrix} $$Rotation in high dimensions
For RoPE to work in higher dimensions, we split the embedding into pairs of dimensions called sub-spaces. This is important because the rotation in the complex plane naturally applies to pairs of dimensions. For the embedding $x_{i} \in \mathbb{R}$ where $d$ is even and $x_{i} = {(x_{1}, x_{2}, x_{3}, ... x_{d})}$, we will have $d/2$ sub-spaces. Each of the sub-spaces is rotated independently in the complex space.
Restructuring the inner product:
$$ f_{q,k}(x_m, m) = R_{\Theta, m}^d W_{(q,k)} x_m $$where:
$$ R_{\Theta,m}^d = \begin{pmatrix} \cos m\theta_1 & -\sin m\theta_1 & 0 & 0 & \cdots & 0 & 0 \\ \sin m\theta_1 & \cos m\theta_1 & 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & \cos m\theta_2 & -\sin m\theta_2 & \cdots & 0 & 0 \\ 0 & 0 & \sin m\theta_2 & \cos m\theta_2 & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & \cos m\theta_{d/2} & -\sin m\theta_{d/2} \\ 0 & 0 & 0 & 0 & \cdots & \sin m\theta_{d/2} & \cos m\theta_{d/2} \end{pmatrix} $$is the rotary matrix with pre-defined parameters $\Theta = \left\{ \theta_i = 10000^{-2(i-1)/d}, \quad i \in [1, 2, \dots, d/2] \right\}$.
As observed the rotation matrix is sparse and it will be computational inefficient considering most operations will be multiplications by zero.
For efficiency, we avoid constructing this sparse matrix directly. Instead, we compute the rotation as:
$$ R_{\Theta, m}^d x = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ \vdots \\ x_{d-1} \\ x_d \end{pmatrix} \otimes \begin{pmatrix} \cos m\theta_1 \\ \cos m\theta_1 \\ \cos m\theta_2 \\ \cos m\theta_2 \\ \vdots \\ \cos m\theta_{d/2} \\ \cos m\theta_{d/2} \end{pmatrix} + \begin{pmatrix} -x_2 \\ x_1 \\ -x_4 \\ x_3 \\ \vdots \\ -x_d \\ x_{d-1} \end{pmatrix} \otimes \begin{pmatrix} \sin m\theta_1 \\ \sin m\theta_1 \\ \sin m\theta_2 \\ \sin m\theta_2 \\ \vdots \\ \sin m\theta_{d/2} \\ \sin m\theta_{d/2} \end{pmatrix} $$Applying our RoPE to self-attention:
$$ q_m^T k_n = (R_{d, \Theta, m} W_q x_m)^T (R_{d, \Theta, n} W_k x_n) = x_m^T W_q^T R_{\Theta, n-m} W_k x_n $$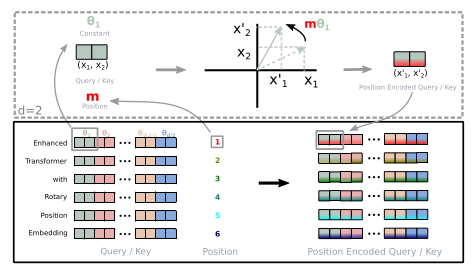
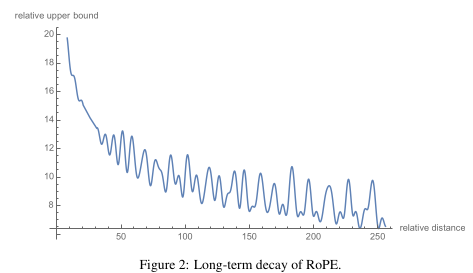
Long term decay
RoPE encodes the relative positional difference $m -n$ into the dot product between the query $q_m$ and $k_n$. The attention mechanism computes:
$$ q_m^T k_n \propto \cos((m-n)\theta) + i\sin((m-n)\theta) $$The term $cos((m-n)\theta)$ decays as $m-n$ grows. For large positional differences $∣m−n∣$, the cosine oscillates rapidly and its contribution to the dot product diminishes when averaged over many dimensions. Meaning - tokens far apart become less correlated. THis causes the attention weight to also drop.
References
- Su, Jianlin, et al. RoFormer: Enhanced Transformer with Rotary Position Embedding. arXiv preprint arXiv:2104.09864 (2021).
- Vaswani, Ashish, et al. Attention is All You Need. Advances in Neural Information Processing Systems. 2017.
- Gehring, Jonas, et al. Convolutional Sequence to Sequence Learning. Proceedings of the 34th International Conference on Machine Learning. 2017.
- Clark, Kevin, et al. What Does BERT Look at? An Analysis of BERT’s Attention. arXiv preprint arXiv:1906.04341 (2019).
- Strang, Gilbert. Introduction to Linear Algebra. Wellesley-Cambridge Press, 2016.
- Youtube tutorial Jak-zee